Алгоритм Беллмана-Форда
Определение
Алгоритм Беллмана-Форда используется для нахождения кратчайших путей от одной начальной вершины до всех остальных вершин во взвешенном ориентированном графе, даже если в нем присутствуют ребра с отрицательными весами.
Алгоритм
- Инициализация: Установите расстояние от начальной вершины до всех остальных вершин равным бесконечности, за исключением начальной вершины, у которой расстояние равно 0.
- Релаксация ребер: Проходите по всем ребрам графа и обновляйте расстояния до каждой вершины, если найден более короткий путь через текущее ребро. Для каждого ребра (u, v) с весом w, обновите расстояние до вершины v как min(distance[v], distance[u] + w).
- Повторение: Повторите шаг 2 n-1 раз, где n - количество вершин в графе. Это необходимо для того, чтобы гарантировать нахождение всех кратчайших путей.
- Проверка наличия циклов с отрицательным весом: После n-1 итераций проверьте все ребра еще раз. Если какое-либо ребро может быть релаксировано, это означает наличие цикла с отрицательным весом в графе.
- Завершение: По завершении работы алгоритма, расстояния от начальной вершины до всех остальных будут содержаться в массиве distance.
Алгоритм Беллмана-Форда может быть использован для нахождения кратчайших путей в графах с отрицательными ребрами, но его сложность составляет O(V*E), где V - количество вершин, E - количество ребер.
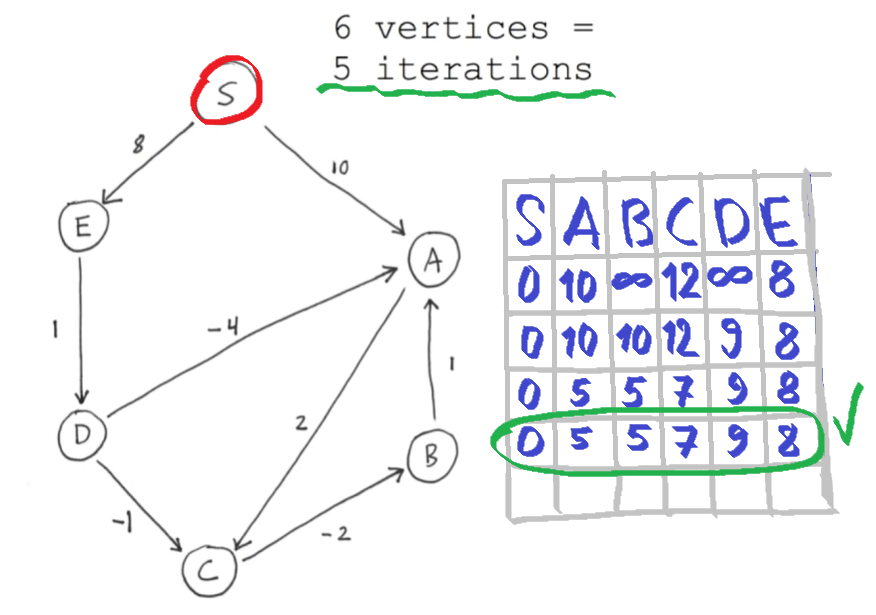
Пример