Алгоритм Флойда-Уоршалла.
Определение
Алгоритм Флойда-Уоршалла используется для нахождения кратчайших путей между всеми парами вершин во взвешенном ориентированном графе, даже если в нем присутствуют ребра с отрицательными весами.
Алгоритм
- Инициализация: Создайте матрицу смежности для графа, где каждый элемент a[i][j] представляет собой вес ребра между вершинами i и j. Если между вершинами нет ребра, то a[i][j] устанавливается как бесконечность. Затем установите диагональные элементы матрицы равными 0.
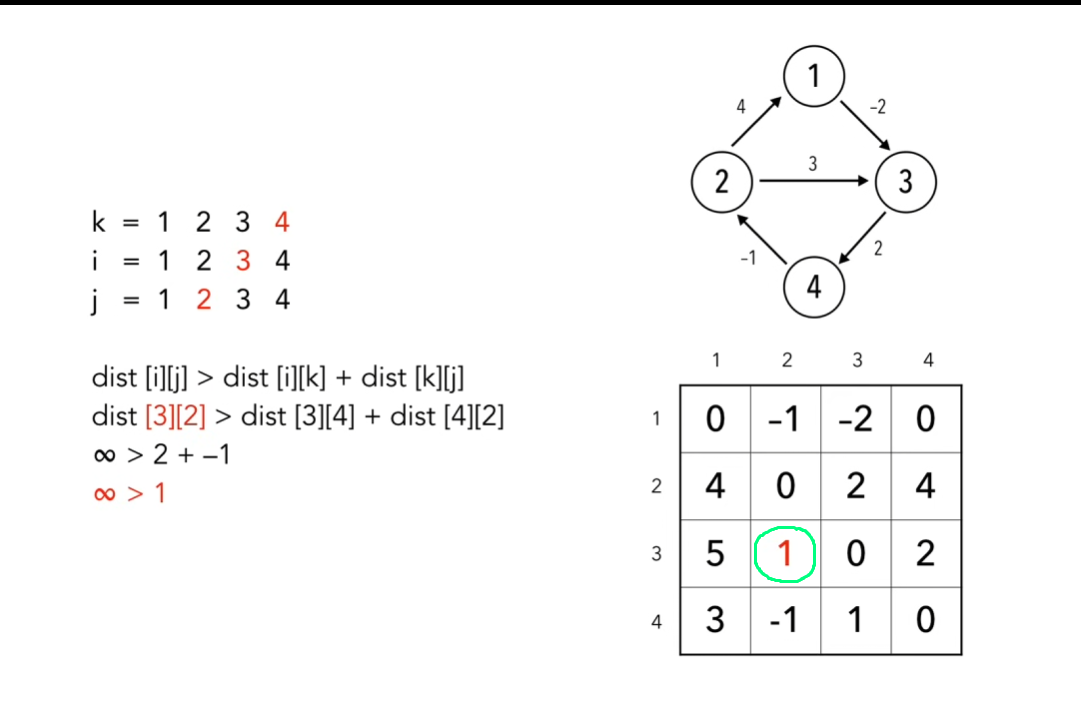
- Обновление расстояний: Для каждой пары вершин (i, j) проверьте, проходит ли путь через вершину k (от 1 до n, где n - количество вершин) быстрее, чем текущий известный путь между вершинами i и j. Если да, обновите значение a[i][j] на минимальное из (a[i][j], a[i][k] + a[k][j]).
- Повторение: Шаг 2 повторяется для каждой пары вершин (i, j) с использованием каждой вершины k.
- Завершение: По завершении работы алгоритма, матрица смежности будет содержать кратчайшие расстояния между всеми парами вершин.
Алгоритм Флойда-Уоршалла работает для всех типов графов, включая графы с отрицательными ребрами, и может быть использован для поиска кратчайших путей между всеми парами вершин в графе.
Сложность O(n^3), n - число вершин (рассматривается каждая пара это n^2, + пытаемся провести эту пару через каждую из вершин это n, и того n^3)
Код
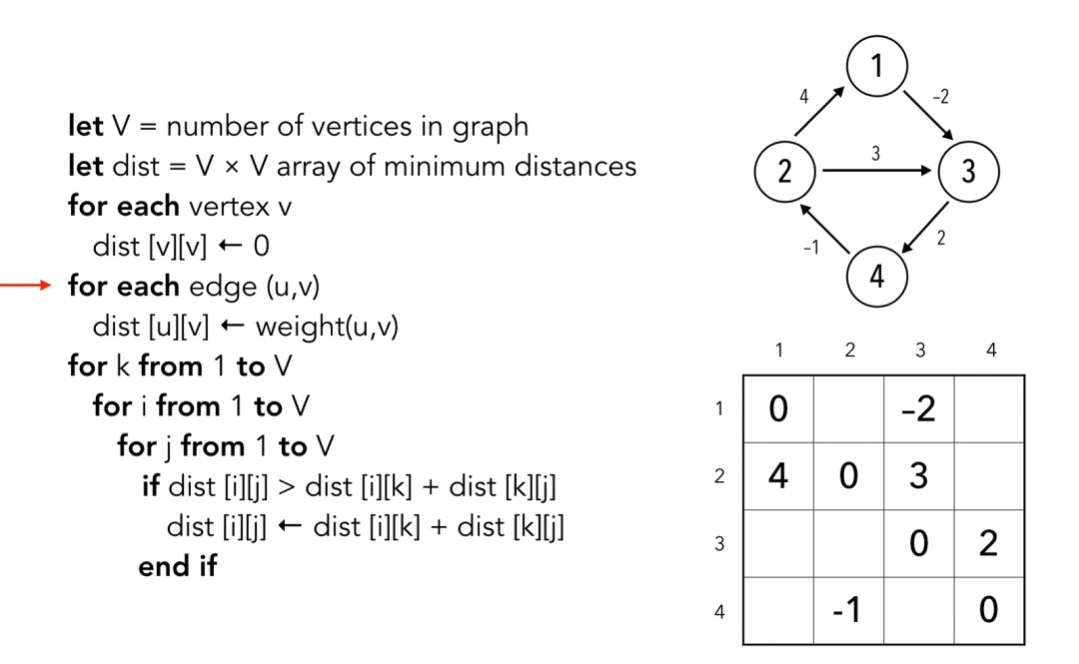
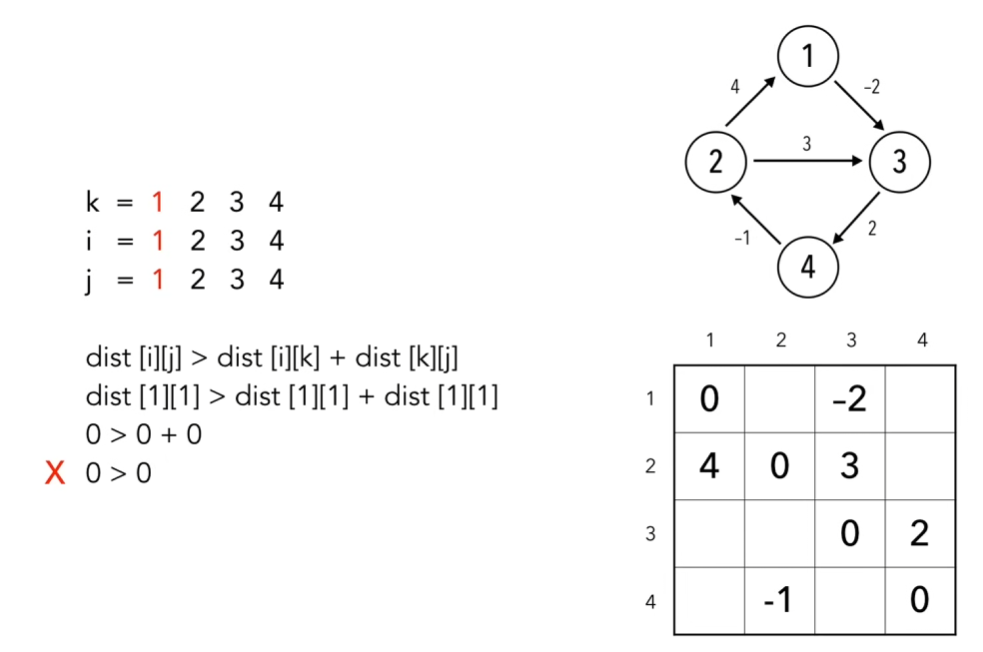
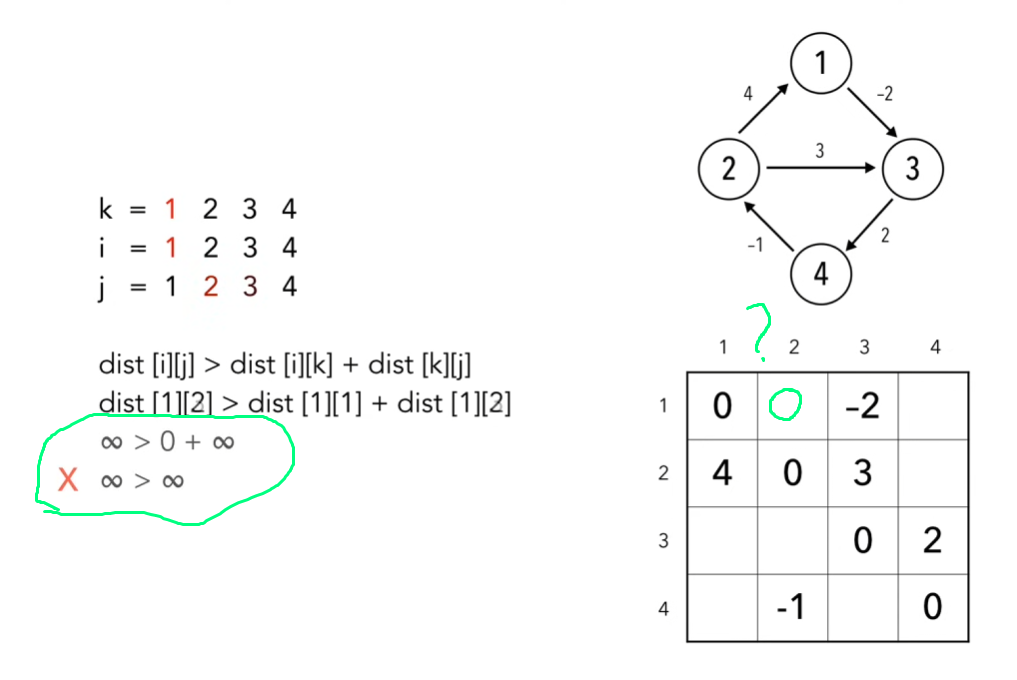
Пример
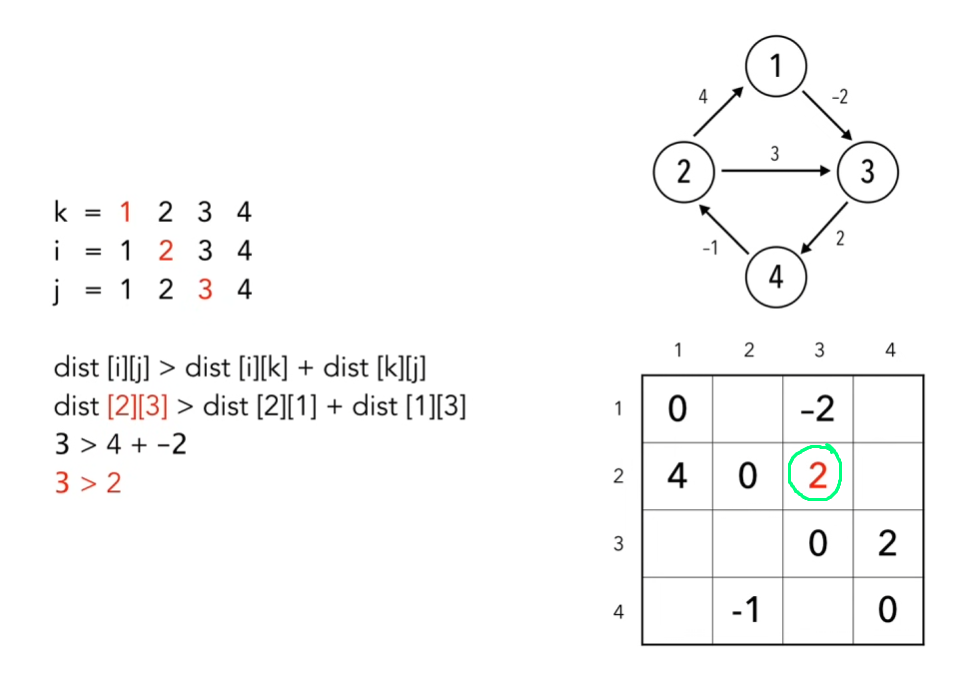
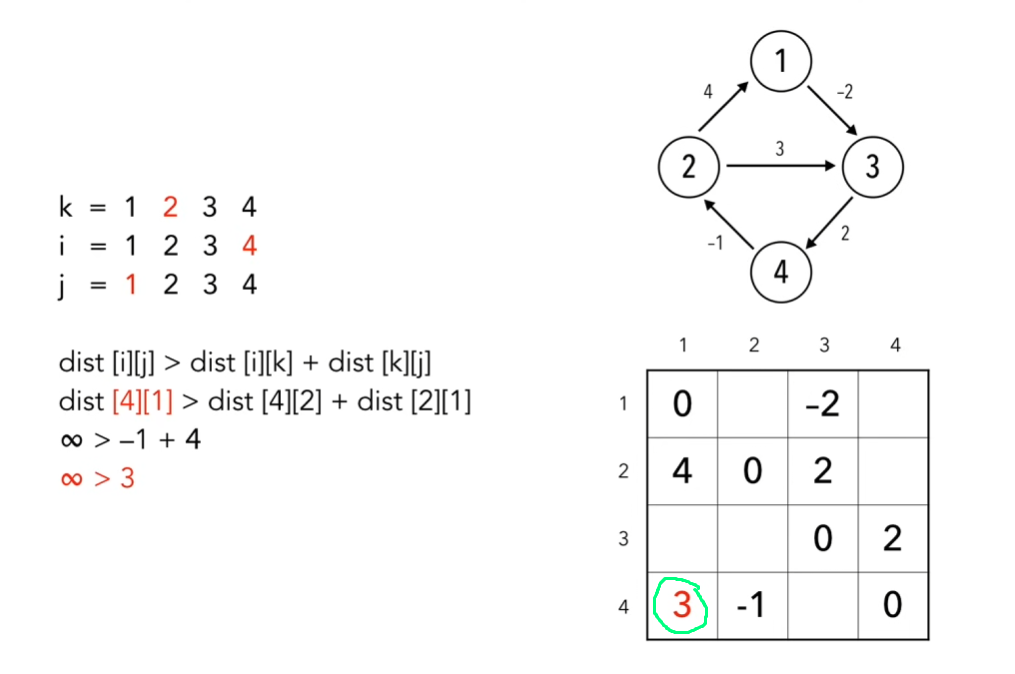
Бла Бла Бла...