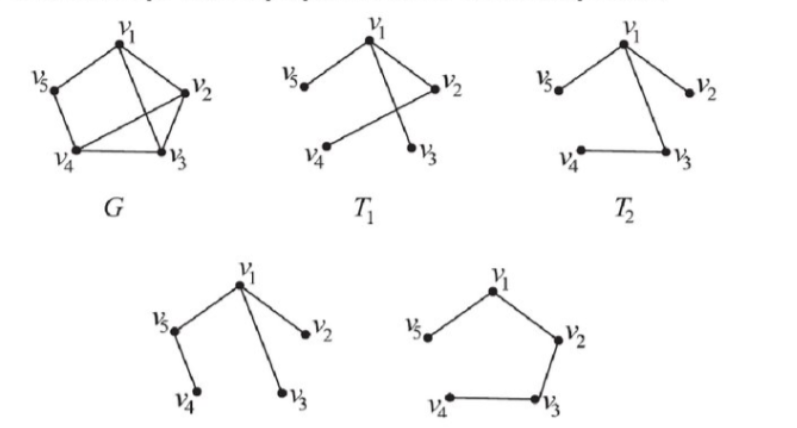
Остовные деревья. Свойства MST.
Определение
Остовное дерево (Минимальное связующее дерево, MST) в графе - это подграф, который является деревом (связным и ациклическим) и содержит все вершины из исходного графа, связывая их минимально возможным количеством ребер.
Свойства MST
- Минимальность по весу: MST содержит ребра, сумма весов которых минимальна среди всех возможных остовных деревьев для данного графа. То есть, сумма весов ребер в MST минимальна.
- Связность: MST связывает все вершины исходного графа, то есть, любые две вершины в графе можно достичь из друг друга, перемещаясь только по ребрам MST.
- Единственность (в общем случае): Если веса всех ребер графа различны, то MST единственно. Однако, если есть несколько ребер с одинаковыми весами, могут существовать различные MST.
- Свойство отсутствия циклов: MST является ациклическим (не содержит циклов), так как любой цикл может быть удален из дерева, не нарушив его связность.
- Связь с кратчайшими путями: MST в графе также связано с кратчайшими путями между вершинами. Например, любое ребро, не включенное в MST, является частью какого-то кратчайшего пути между двумя вершинами.
- Графы с положительными весами: Для графов с положительными весами существует простой алгоритм для нахождения MST - алгоритм Прима или алгоритм Краскала.
- Графы с отрицательными весами: Для графов с отрицательными весами существуют другие алгоритмы, такие как алгоритм Борувки или алгоритм Дейкстры с модификацией. При создании карты сайта с древовидной системой разделов.