Динамическое программирование. Задача о количестве маршрутов. Принцип Беллмана.
Определение
Динамическое программирование - это метод решения оптимизационных задач, в которых решение можно разбить на более мелкие подзадачи, которые, в свою очередь, также можно разбить на еще более мелкие подзадачи. При этом решение каждой подзадачи используется для решения более крупных подзадач, пока не будет найдено решение всей задачи в целом.
Динамическое программирование похоже на метод «разделяй и властвуй» оба из которых решают исходную проблему путем решения подзадач. Разница в том, что алгоритм «разделяй и властвуй» будет выполнять много ненужной работы при решении подзадач, он будет многократно решать эти общие подзадачи; в то время как алгоритм динамического программирования решает каждую подзадачу только один раз, и сохраняет свое решение.
В рекурсии например результаты подзадач используется при формировании ответа, но никак не помогают при решении подзадач.
Что эффективнее?
- рекурсия с ответом: return fibo(n-1) + fibo(n-2) без мемоизации
- последовательное вычисление каждого числа фибоначчи, но ровно 1 раз.
Принцип оптимальности Беллмана: алгоритм считается оптимальным, если на любом его шаге для получения оптимального решения, используется результат его предыдущих решений.
Задача
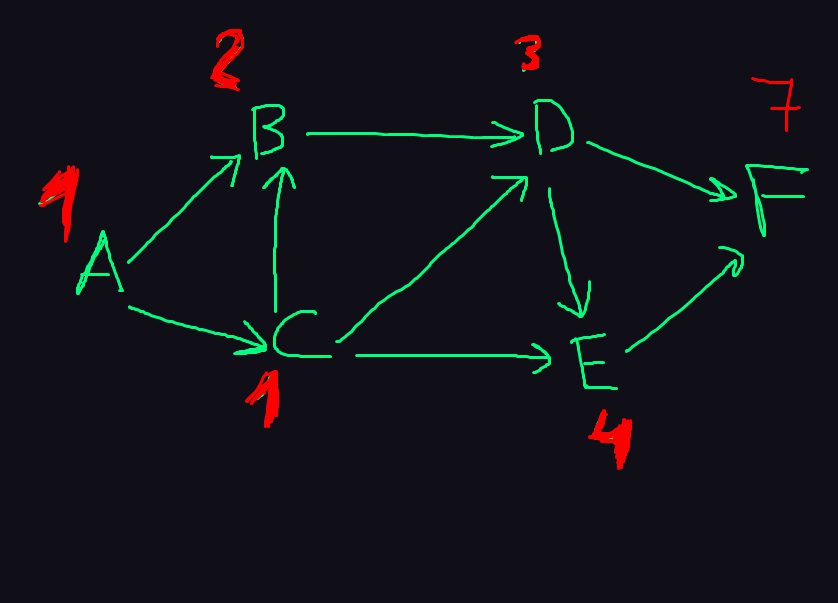
Задача о количестве маршрутов: имеются несколько городов и между некоторыми из них проведены односторонние дороги так, что выехав из города, вернуться по той же дороге невозможно. Требуется найти кол-во маршрутов из одного пункта в другой.
Идея: чтобы подсчитать кол-во путей до пункта, необходимо знать сколькими способами мы можем попасть в пункты ведущие в этот и т.д.
Ход алгоритма:
- устанавливаем значение стартовой вершины 1
- проходимся по графу, например в матрице смежности и устанавливаем значение вершины как сумма значений вершин, которые ведут в неё